https://julius.co.jp/info/himeji/4618/

前回の、作図問題の解答です。

—————————————————————————-

最終的には、こんな感じの４等分を目指すことになります。

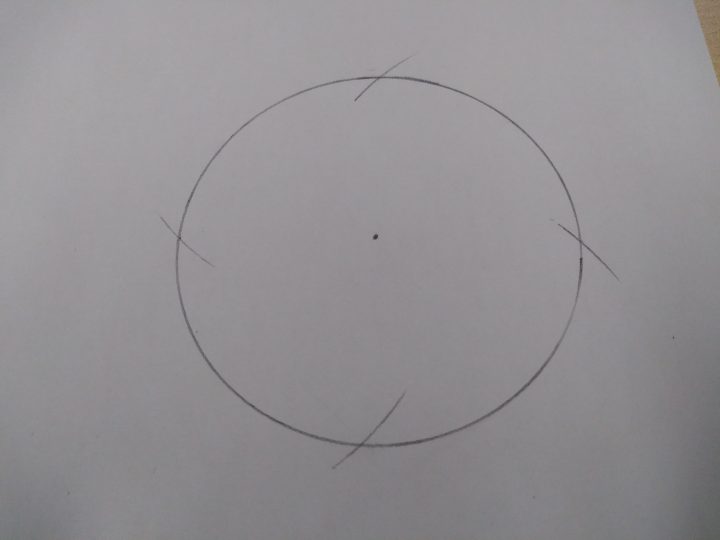
ここで、三角形に注目してみると、円の半径を１としたときの√２にあたる長さがコンパスで調べられたら、４等分がうまくいくことが分かりますね。

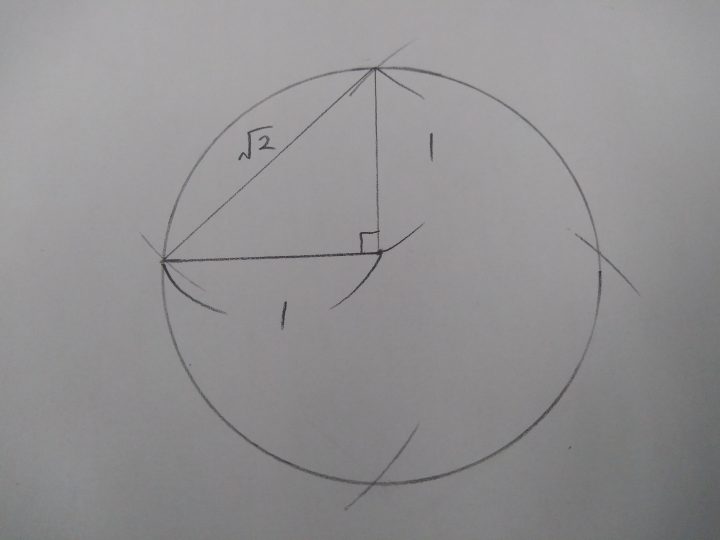
というわけで、スタートです。
まずは、円周上の任意の点から、半径と同じ１の長さで区切っていきます。６等分できますね。（実際には全部切る必要はありませんが。）

ここで、３つの点に注目し、三角形の辺の長さを考えます。
すると、直径に対する円周角が直角になることから、1:2:√3の三角形であることが分かりますね。（三平方の定理）

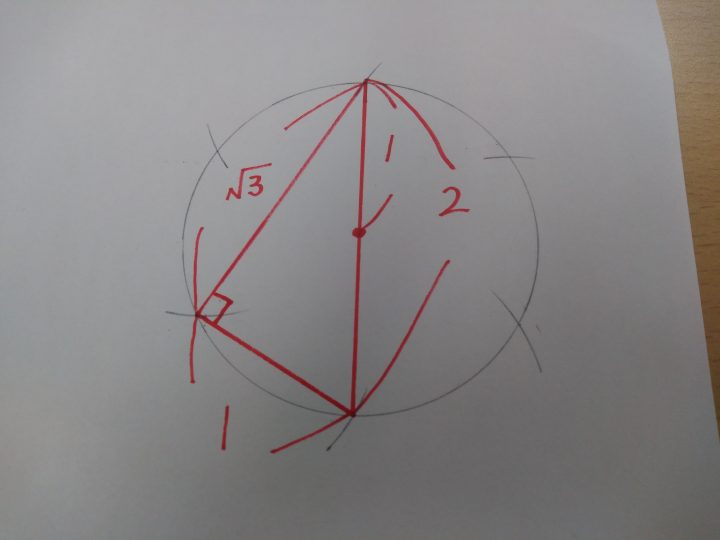
コンパスで、その√３の長さを取り、円の直径の端と端から等距離の点を取ります。

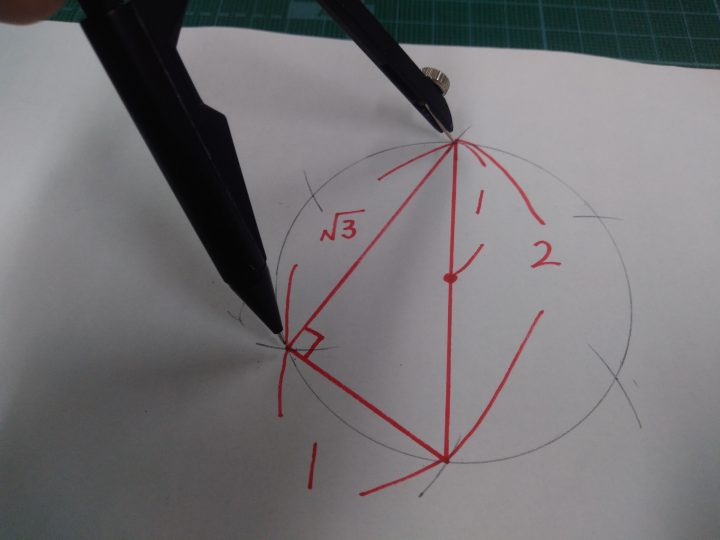
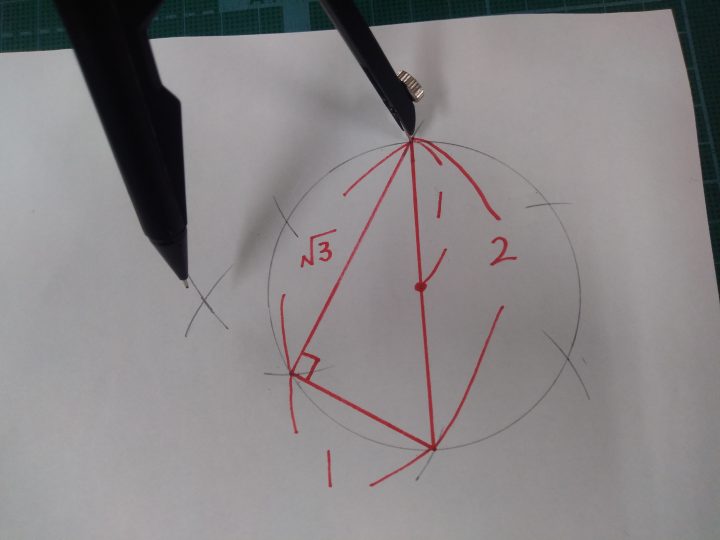
次に、その点を頂点の１つとする三角形（下図の緑色部分）に注目すると、三平方の定理から、√２を導くことができます。

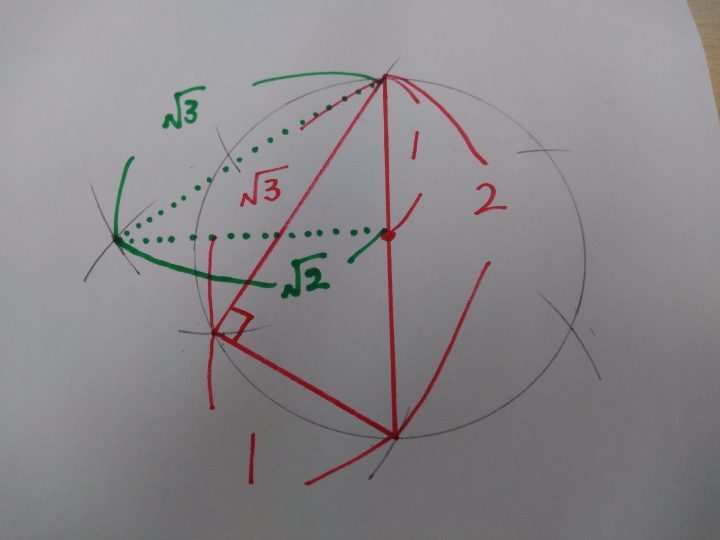
あとは、この√２をコンパスで取って、円周上の任意の点から順に切り取っていけば４等分の完了です。

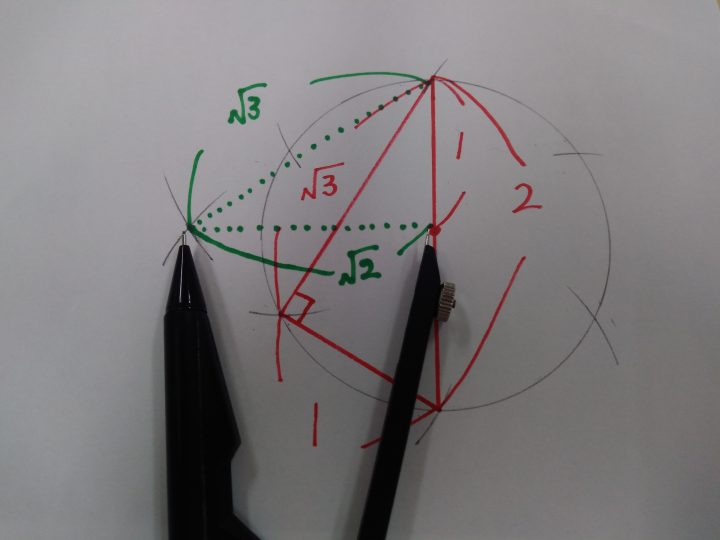
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　姫路教室　　宇崎